CURSO BÁSICO DE MATEMÁTICA FINANCEIRA – PARTE 01 – JUROS
Página 1 de 1
 CURSO BÁSICO DE MATEMÁTICA FINANCEIRA – PARTE 01 – JUROS
CURSO BÁSICO DE MATEMÁTICA FINANCEIRA – PARTE 01 – JUROS
CURSO BÁSICO DE MATEMÁTICA FINANCEIRA – PARTE 01 – JUROS
Desenvolvido por: Celso Andrade
JURO
Segundo o Dicionário Aurélio:
Juro
[Do lat. jure.]
S.m.
FATOR DE FORMAÇÃO DE JUROS
O valor do juro é obtido aplicando-se a taxa de juros sobre um valor. A taxa é representada na forma percentual e o valor a que este percentual incide pode ser o valor aplicado (inicial de um investimento), o valor original de uma prestação, ou seja, sobre qualquer valor.

Exemplo:
A partir deste fator, podemos determinar o capital corrigido, que é o resultado da soma do valor inicial com o valor do juro.
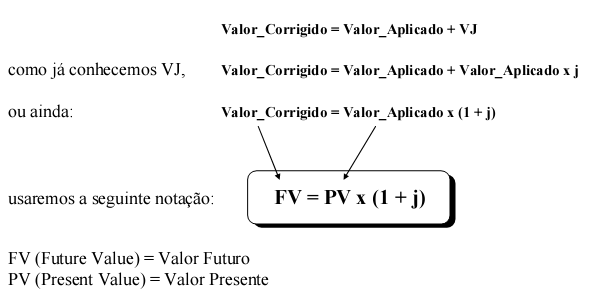
As siglas são em inglês, pois é como encontramos na maioria das calculadoras, planilhas eletrônicas e softwares.
Utilizando as informações do exemplo anterior:
Da mesma forma, podemos aplicar este conceito na variação dos preços dos produtos:
No lugar de FV obteremos o preço corrigido e no lugar de PV usaremos o preço atual.
JURO SIMPLES
O juro simples é calculado somente sobre o capital, não havendo interferência dos juros passados em seu cálculo.
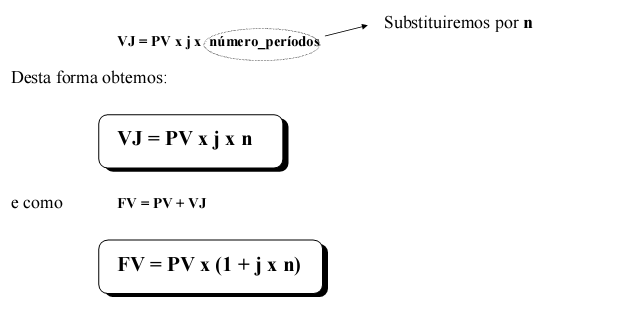
O valor calculado a partir do juro simples é resultante da multiplicação do fator de juros pelo valor inicial e pelo número de períodos.
Exemplo:
Se imaginarmos uma caderneta de poupança, cujo titular faz saques mensais no exato valor dos juros creditados, teremos um caso prático de juro simples, pois o valor do juro é calculado sempre sobre o capital aplicado.
Exemplificando:
(e assim por diante...)
JURO COMPOSTO
O juro composto é calculado com base no capital e nos juros passados. Também é conhecidos como juro capitalizado.
Exemplificando:
Vamos imaginar um empréstimo de R$ 100.000,00 com uma taxa de 5 %a.m. Por 3 meses com um único pagamento no final.
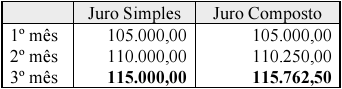
Como vimos anteriormente, o juro simples é calculado somente sobre o capital, portanto, o valor devido é de R$ 115.000,00 =>100.000,00 x (1 + 0,05 x 3).
Porém no juro composto, o cálculo é feito sobre o saldo devedor:
1 mês => 100.000,00 x (1 +0,05) = 105.000,00
2 mês => 105.000,00 x (1 +0,05) = 110.250,00
3 mês => 110.250,00 x (1 +0,05) = 115.762,50
ou seja,
115.762,50 = 100.000,00 x 1,05 x 1,05 x 1,053
115.762,50 = 100.000,00 x (1,05) ^ 3
De uma forma genérica:

Para calcularmos somente o juro é necessário que o capital seja desconsiderado:
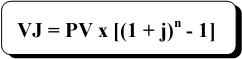
O mesmo cálculo utilizando juro composto: Se uma determinada aplicação rende 5% a.m., qual o valor do juro em 4 meses, para R$ 10.000,00 aplicados e qual o valor no futuro?
R1.: VJ =10.000,00 x [(1 + 0,05) ^ 4 - 1] => VJ = R$ 2.155,06
R2.: FV = 10.000,00 x (1 + 0,05) ^ 4 => FV = R$ 12.155,06
EQUIVALÊNCIA DA TAXA DE JUROS
Taxas de juros equivalentes são aquelas que representam a mesma taxa em um determinado período, ou seja, uma taxa expressa ao ano possui uma taxa equivalente em 2 anos, uma em 3 anos, outra em 1 dia,s endo que todas são equivalentes entre si.
Para calcularmos a taxa equivalente devemos levar a taxa da base original para a base
desejada (a base original é a base em que a taxa está expressa) .
Para Juro Simples:

Para Juro Composto:

Exemplificando:
10 % em 2 períodos
Para Juro Simples:
Taxa_Equivalente_2_Períodos = (0,10 / 1) x 2 => 20,000 %
em outras palavras, 20 % em dois períodos equivale a 10 % em um período
Para Juro Composto:
Taxa_Equivalente_2_Períodos = ((1 + 0,10) ^ (2 / 1)) - 1 => 21,000 %
em outras palavras, 21 % em dois períodos equivale a 10 % em um período
No mercado financeiro brasileiro as taxas equivalentes são calculadas no modo composto, enquanto que na maioria dos países são calculadas no modo simples.
Desenvolvido por: Celso Andrade
JURO
Segundo o Dicionário Aurélio:
Juro
[Do lat. jure.]
S.m.
- Lucro, calculado sobre determinada taxa, de dinheiro emprestado ou de capital empregado; rendimento, interesse. [Sin. (bras., RJ, gír.): jurema.]
- Fam. Recompensa(2).
- Ant. Jus, direito. Juro composto: O que se soma ao capital para o cálculo de novos juros nos tempos seguintes. Juro simples: O que não se soma ao capital para o cálculo de novos juros nos tempos seguintes. Pagar com juros. Bras.: Pagar caro.
FATOR DE FORMAÇÃO DE JUROS
O valor do juro é obtido aplicando-se a taxa de juros sobre um valor. A taxa é representada na forma percentual e o valor a que este percentual incide pode ser o valor aplicado (inicial de um investimento), o valor original de uma prestação, ou seja, sobre qualquer valor.

Exemplo:
- Uma determinada aplicação rende 5% a.m.(ao mês), qual o valor do juro em um mês, para R$ 10.000,00 aplicados?
R.: VJ =10.000,00 x 0,05 => VJ = R$ 500,00
Este conceito pode ser aplicado para calcularmos o aumento de preço de um determinado produto. Basta usar o valor do aumento no lugar do VJ e o valor atual no lugar de VA. - Um comerciante deseja aumentar seus produto sem 4 %. Qual o valor do aumento para um produto que custa R$ 500,00?
R.: V_aumento =500,00 x 0,04 => V_aumento = R$ 20,00
A partir deste fator, podemos determinar o capital corrigido, que é o resultado da soma do valor inicial com o valor do juro.

As siglas são em inglês, pois é como encontramos na maioria das calculadoras, planilhas eletrônicas e softwares.
Utilizando as informações do exemplo anterior:
- Se uma determinada aplicação rende 5% a.m., quanto terá ao final de um mês quem aplicar R$ 10.000,00?
R.: FV=10.000,00 x (1 +0,05) => FV = R$ 10.500,00
Da mesma forma, podemos aplicar este conceito na variação dos preços dos produtos:
No lugar de FV obteremos o preço corrigido e no lugar de PV usaremos o preço atual.
- Um comerciante deseja aumentar seus produtos em 4 %. Qual o novo valor de um produto que custa atualmente R$ 500,00?
R.: FV=500,00x (1+0,04) => FV = R$ 520,00
JURO SIMPLES
O juro simples é calculado somente sobre o capital, não havendo interferência dos juros passados em seu cálculo.
O valor calculado a partir do juro simples é resultante da multiplicação do fator de juros pelo valor inicial e pelo número de períodos.

Exemplo:
- Se uma determinada aplicação rende 5% a.m., qual o valor do juro em 4 meses, para R$ 10.000,00 aplicados e qual o valor no futuro?
R1.: VJ =10.000,00 x 0,05 x 4 => VJ = R$ 2.000,00
R2.: FV=10.000,00 x (1 +0,05 x 4) => FV= R$ 12.000,00
Se imaginarmos uma caderneta de poupança, cujo titular faz saques mensais no exato valor dos juros creditados, teremos um caso prático de juro simples, pois o valor do juro é calculado sempre sobre o capital aplicado.
Exemplificando:
| Aplicação | = | 5.000,00 | |
| Rendimento3,0% | = | 150,00 | => (5.000,00 x 0,030) |
| Saque | = | 150,00 | |
| Rendimento2,5% | = | 125,00 | => (5.000,00 x 0,025) |
| Saque | = | 125,00 |
JURO COMPOSTO
O juro composto é calculado com base no capital e nos juros passados. Também é conhecidos como juro capitalizado.
Exemplificando:
Vamos imaginar um empréstimo de R$ 100.000,00 com uma taxa de 5 %a.m. Por 3 meses com um único pagamento no final.

Como vimos anteriormente, o juro simples é calculado somente sobre o capital, portanto, o valor devido é de R$ 115.000,00 =>100.000,00 x (1 + 0,05 x 3).
Porém no juro composto, o cálculo é feito sobre o saldo devedor:
1 mês => 100.000,00 x (1 +0,05) = 105.000,00
2 mês => 105.000,00 x (1 +0,05) = 110.250,00
3 mês => 110.250,00 x (1 +0,05) = 115.762,50
ou seja,
115.762,50 = 100.000,00 x 1,05 x 1,05 x 1,053
115.762,50 = 100.000,00 x (1,05) ^ 3
De uma forma genérica:

Para calcularmos somente o juro é necessário que o capital seja desconsiderado:
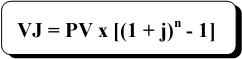
O mesmo cálculo utilizando juro composto: Se uma determinada aplicação rende 5% a.m., qual o valor do juro em 4 meses, para R$ 10.000,00 aplicados e qual o valor no futuro?
R1.: VJ =10.000,00 x [(1 + 0,05) ^ 4 - 1] => VJ = R$ 2.155,06
R2.: FV = 10.000,00 x (1 + 0,05) ^ 4 => FV = R$ 12.155,06
EQUIVALÊNCIA DA TAXA DE JUROS
Taxas de juros equivalentes são aquelas que representam a mesma taxa em um determinado período, ou seja, uma taxa expressa ao ano possui uma taxa equivalente em 2 anos, uma em 3 anos, outra em 1 dia,s endo que todas são equivalentes entre si.
Para calcularmos a taxa equivalente devemos levar a taxa da base original para a base
desejada (a base original é a base em que a taxa está expressa) .
Para Juro Simples:

Para Juro Composto:

Exemplificando:
10 % em 2 períodos
Para Juro Simples:
Taxa_Equivalente_2_Períodos = (0,10 / 1) x 2 => 20,000 %
em outras palavras, 20 % em dois períodos equivale a 10 % em um período
Para Juro Composto:
Taxa_Equivalente_2_Períodos = ((1 + 0,10) ^ (2 / 1)) - 1 => 21,000 %
em outras palavras, 21 % em dois períodos equivale a 10 % em um período
No mercado financeiro brasileiro as taxas equivalentes são calculadas no modo composto, enquanto que na maioria dos países são calculadas no modo simples.
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos